반응형
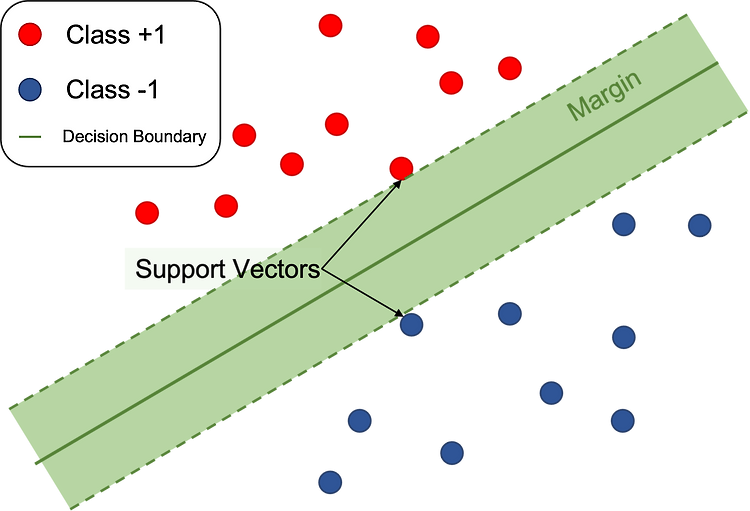
서포트벡터머신 - 이진분류
- 피마인디언 당뇨병 데이터셋
In [3]:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
1. 데이터 준비
In [4]:
from google.colab import drive
drive.mount('/content/drive')
Drive already mounted at /content/drive; to attempt to forcibly remount, call drive.mount("/content/drive", force_remount=True).
In [5]:
df = pd.read_csv("/content/drive/MyDrive/SKT FLY AI/2주차/diabetes.csv")
In [6]:
df.head()
Out[6]:
| Pregnancies | Glucose | BloodPressure | SkinThickness | Insulin | BMI | DiabetesPedigreeFunction | Age | Outcome | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 148 | 72 | 35 | 0 | 33.6 | 0.627 | 50 | 1 |
| 1 | 1 | 85 | 66 | 29 | 0 | 26.6 | 0.351 | 31 | 0 |
| 2 | 8 | 183 | 64 | 0 | 0 | 23.3 | 0.672 | 32 | 1 |
| 3 | 1 | 89 | 66 | 23 | 94 | 28.1 | 0.167 | 21 | 0 |
| 4 | 0 | 137 | 40 | 35 | 168 | 43.1 | 2.288 | 33 | 1 |
In [7]:
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 768 entries, 0 to 767
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Pregnancies 768 non-null int64
1 Glucose 768 non-null int64
2 BloodPressure 768 non-null int64
3 SkinThickness 768 non-null int64
4 Insulin 768 non-null int64
5 BMI 768 non-null float64
6 DiabetesPedigreeFunction 768 non-null float64
7 Age 768 non-null int64
8 Outcome 768 non-null int64
dtypes: float64(2), int64(7)
memory usage: 54.1 KB
In [8]:
df.describe().T
Out[8]:
| count | mean | std | min | 25% | 50% | 75% | max | |
|---|---|---|---|---|---|---|---|---|
| Pregnancies | 768.0 | 3.845052 | 3.369578 | 0.000 | 1.00000 | 3.0000 | 6.00000 | 17.00 |
| Glucose | 768.0 | 120.894531 | 31.972618 | 0.000 | 99.00000 | 117.0000 | 140.25000 | 199.00 |
| BloodPressure | 768.0 | 69.105469 | 19.355807 | 0.000 | 62.00000 | 72.0000 | 80.00000 | 122.00 |
| SkinThickness | 768.0 | 20.536458 | 15.952218 | 0.000 | 0.00000 | 23.0000 | 32.00000 | 99.00 |
| Insulin | 768.0 | 79.799479 | 115.244002 | 0.000 | 0.00000 | 30.5000 | 127.25000 | 846.00 |
| BMI | 768.0 | 31.992578 | 7.884160 | 0.000 | 27.30000 | 32.0000 | 36.60000 | 67.10 |
| DiabetesPedigreeFunction | 768.0 | 0.471876 | 0.331329 | 0.078 | 0.24375 | 0.3725 | 0.62625 | 2.42 |
| Age | 768.0 | 33.240885 | 11.760232 | 21.000 | 24.00000 | 29.0000 | 41.00000 | 81.00 |
| Outcome | 768.0 | 0.348958 | 0.476951 | 0.000 | 0.00000 | 0.0000 | 1.00000 | 1.00 |
In [9]:
df.Outcome.value_counts()
Out[9]:
0 500
1 268
Name: Outcome, dtype: int642. 테스트데이터 분리¶
In [10]:
y = df.Outcome
y
Out[10]:
0 1
1 0
2 1
3 0
4 1
..
763 0
764 0
765 0
766 1
767 0
Name: Outcome, Length: 768, dtype: int64In [11]:
X = df.drop('Outcome',axis=1)
X
Out[11]:
| Pregnancies | Glucose | BloodPressure | SkinThickness | Insulin | BMI | DiabetesPedigreeFunction | Age | |
|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 148 | 72 | 35 | 0 | 33.6 | 0.627 | 50 |
| 1 | 1 | 85 | 66 | 29 | 0 | 26.6 | 0.351 | 31 |
| 2 | 8 | 183 | 64 | 0 | 0 | 23.3 | 0.672 | 32 |
| 3 | 1 | 89 | 66 | 23 | 94 | 28.1 | 0.167 | 21 |
| 4 | 0 | 137 | 40 | 35 | 168 | 43.1 | 2.288 | 33 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 763 | 10 | 101 | 76 | 48 | 180 | 32.9 | 0.171 | 63 |
| 764 | 2 | 122 | 70 | 27 | 0 | 36.8 | 0.340 | 27 |
| 765 | 5 | 121 | 72 | 23 | 112 | 26.2 | 0.245 | 30 |
| 766 | 1 | 126 | 60 | 0 | 0 | 30.1 | 0.349 | 47 |
| 767 | 1 | 93 | 70 | 31 | 0 | 30.4 | 0.315 | 23 |
768 rows × 8 columns
In [12]:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.2, random_state = 42,stratify=y)
In [13]:
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
(614, 8) (154, 8) (614,) (154,)
In [14]:
y_train.value_counts()
Out[14]:
0 400
1 214
Name: Outcome, dtype: int64In [15]:
y_test.value_counts()
Out[15]:
0 100
1 54
Name: Outcome, dtype: int643. 전처리
결측치 체크
In [16]:
X_train.isna().sum()
Out[16]:
Pregnancies 0
Glucose 0
BloodPressure 0
SkinThickness 0
Insulin 0
BMI 0
DiabetesPedigreeFunction 0
Age 0
dtype: int64이상치 체크
- 0인값을 가진 샘플을 지우기
In [17]:
df1 = X_train.copy()
df1.shape
Out[17]:
(614, 8)In [18]:
df1.columns
Out[18]:
Index(['Pregnancies', 'Glucose', 'BloodPressure', 'SkinThickness', 'Insulin',
'BMI', 'DiabetesPedigreeFunction', 'Age'],
dtype='object')In [19]:
cols = ['Glucose', 'BloodPressure', 'SkinThickness', 'Insulin',
'BMI']
In [20]:
df1 = df1[cols].replace(0,np.nan) # 0을 결측치로 대체
df1.isna().sum()
Out[20]:
Glucose 4
BloodPressure 23
SkinThickness 175
Insulin 290
BMI 9
dtype: int64In [21]:
df1 = df1.dropna()
df1.shape
# 결과값을 봤을 때 데이터의 유실이 너무 많음 -> 다른 방안으로 대체
Out[21]:
(322, 5)- 0인 값을 적당한 값으로 채워넣는 방법 -> median 값으로 대체
In [22]:
df2 = X_train.copy()
df2.shape
Out[22]:
(614, 8)In [23]:
df2[cols] = df2[cols].replace(0,np.nan) # 0을 결측치로 대체
df2.isna().sum()
Out[23]:
Pregnancies 0
Glucose 4
BloodPressure 23
SkinThickness 175
Insulin 290
BMI 9
DiabetesPedigreeFunction 0
Age 0
dtype: int64In [24]:
df2['Glucose'] = df2['Glucose'].fillna(df2['Glucose'].median())
df2['BloodPressure'] = df2['BloodPressure'].fillna(df2['BloodPressure'].median())
df2['SkinThickness'] = df2['SkinThickness'].fillna(df2['SkinThickness'].median())
df2['Insulin'] = df2['Insulin'].fillna(df2['Insulin'].median())
df2['BMI'] = df2['BMI'].fillna(df2['BMI'].median())
In [25]:
G_m = df['Glucose'].median()
B_m = df['BloodPressure'].median()
S_m = df['SkinThickness'].median()
I_m = df['Insulin'].median()
Bm_m = df['BMI'].median()
In [26]:
df2.describe()
Out[26]:
| Pregnancies | Glucose | BloodPressure | SkinThickness | Insulin | BMI | DiabetesPedigreeFunction | Age | |
|---|---|---|---|---|---|---|---|---|
| count | 614.000000 | 614.000000 | 614.000000 | 614.000000 | 614.000000 | 614.000000 | 614.000000 | 614.000000 |
| mean | 3.819218 | 121.671010 | 72.140065 | 29.042345 | 137.705212 | 32.448208 | 0.477428 | 33.366450 |
| std | 3.314148 | 30.003794 | 12.275119 | 8.891855 | 78.764767 | 6.824122 | 0.330300 | 11.833438 |
| min | 0.000000 | 56.000000 | 24.000000 | 7.000000 | 15.000000 | 18.200000 | 0.084000 | 21.000000 |
| 25% | 1.000000 | 99.000000 | 64.000000 | 25.000000 | 120.000000 | 27.625000 | 0.245000 | 24.000000 |
| 50% | 3.000000 | 117.000000 | 72.000000 | 29.000000 | 125.000000 | 32.400000 | 0.382500 | 29.000000 |
| 75% | 6.000000 | 140.000000 | 80.000000 | 32.000000 | 130.000000 | 36.500000 | 0.639250 | 41.000000 |
| max | 17.000000 | 199.000000 | 122.000000 | 99.000000 | 744.000000 | 67.100000 | 2.329000 | 81.000000 |
In [27]:
df2[cols] = df2[cols].fillna(df[cols])
In [28]:
df2.describe()
Out[28]:
| Pregnancies | Glucose | BloodPressure | SkinThickness | Insulin | BMI | DiabetesPedigreeFunction | Age | |
|---|---|---|---|---|---|---|---|---|
| count | 614.000000 | 614.000000 | 614.000000 | 614.000000 | 614.000000 | 614.000000 | 614.000000 | 614.000000 |
| mean | 3.819218 | 121.671010 | 72.140065 | 29.042345 | 137.705212 | 32.448208 | 0.477428 | 33.366450 |
| std | 3.314148 | 30.003794 | 12.275119 | 8.891855 | 78.764767 | 6.824122 | 0.330300 | 11.833438 |
| min | 0.000000 | 56.000000 | 24.000000 | 7.000000 | 15.000000 | 18.200000 | 0.084000 | 21.000000 |
| 25% | 1.000000 | 99.000000 | 64.000000 | 25.000000 | 120.000000 | 27.625000 | 0.245000 | 24.000000 |
| 50% | 3.000000 | 117.000000 | 72.000000 | 29.000000 | 125.000000 | 32.400000 | 0.382500 | 29.000000 |
| 75% | 6.000000 | 140.000000 | 80.000000 | 32.000000 | 130.000000 | 36.500000 | 0.639250 | 41.000000 |
| max | 17.000000 | 199.000000 | 122.000000 | 99.000000 | 744.000000 | 67.100000 | 2.329000 | 81.000000 |
In [29]:
X_train = df2.copy()
스케일링
In [30]:
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train_s = scaler.fit_transform(X_train)
X_train_s
Out[30]:
array([[-0.85135507, -1.05642747, -0.82674004, ..., -0.76969431,
0.31079384, -0.79216928],
[ 0.35657564, 0.14439907, 0.47777235, ..., -0.41771394,
-0.11643851, 0.56103382],
[-0.5493724 , -0.55608308, -1.15286813, ..., 0.35957603,
-0.76486207, -0.70759409],
...,
[-0.85135507, -0.82293342, -0.17448384, ..., 0.82888319,
-0.78607218, -0.28471812],
[ 1.86648903, -0.35594533, -0.17448384, ..., -0.72569676,
-1.01938346, 0.56103382],
[ 0.05459296, 0.74481233, -1.15286813, ..., -0.43237979,
-0.57700104, 0.30730824]])In [31]:
scaler.mean_
Out[31]:
array([ 3.81921824, 121.67100977, 72.14006515, 29.04234528,
137.70521173, 32.44820847, 0.47742834, 33.36644951])In [32]:
y_train = y_train.values
type(y_train)
Out[32]:
numpy.ndarray4. 학습
- SVC 베이스 모델
In [33]:
from sklearn.svm import SVC
clf = SVC(random_state = 42)
clf = clf.fit(X_train_s,y_train)
5. 예측
테스트 데이터 전처리 먼저
- 0인 값을 위에서 계산한 값으로 넣는 작업
- 스케일링
In [34]:
X_test.head(5)
Out[34]:
| Pregnancies | Glucose | BloodPressure | SkinThickness | Insulin | BMI | DiabetesPedigreeFunction | Age | |
|---|---|---|---|---|---|---|---|---|
| 44 | 7 | 159 | 64 | 0 | 0 | 27.4 | 0.294 | 40 |
| 672 | 10 | 68 | 106 | 23 | 49 | 35.5 | 0.285 | 47 |
| 700 | 2 | 122 | 76 | 27 | 200 | 35.9 | 0.483 | 26 |
| 630 | 7 | 114 | 64 | 0 | 0 | 27.4 | 0.732 | 34 |
| 81 | 2 | 74 | 0 | 0 | 0 | 0.0 | 0.102 | 22 |
In [35]:
X_test = X_test.replace(0,np.nan)
X_test
Out[35]:
| Pregnancies | Glucose | BloodPressure | SkinThickness | Insulin | BMI | DiabetesPedigreeFunction | Age | |
|---|---|---|---|---|---|---|---|---|
| 44 | 7.0 | 159.0 | 64.0 | NaN | NaN | 27.4 | 0.294 | 40 |
| 672 | 10.0 | 68.0 | 106.0 | 23.0 | 49.0 | 35.5 | 0.285 | 47 |
| 700 | 2.0 | 122.0 | 76.0 | 27.0 | 200.0 | 35.9 | 0.483 | 26 |
| 630 | 7.0 | 114.0 | 64.0 | NaN | NaN | 27.4 | 0.732 | 34 |
| 81 | 2.0 | 74.0 | NaN | NaN | NaN | NaN | 0.102 | 22 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 32 | 3.0 | 88.0 | 58.0 | 11.0 | 54.0 | 24.8 | 0.267 | 22 |
| 637 | 2.0 | 94.0 | 76.0 | 18.0 | 66.0 | 31.6 | 0.649 | 23 |
| 593 | 2.0 | 82.0 | 52.0 | 22.0 | 115.0 | 28.5 | 1.699 | 25 |
| 425 | 4.0 | 184.0 | 78.0 | 39.0 | 277.0 | 37.0 | 0.264 | 31 |
| 273 | 1.0 | 71.0 | 78.0 | 50.0 | 45.0 | 33.2 | 0.422 | 21 |
154 rows × 8 columns
In [36]:
X_test['Glucose'] = X_test['Glucose'].fillna(G_m)
X_test['BloodPressure'] = X_test['BloodPressure'].fillna(B_m)
X_test['SkinThickness'] = X_test['SkinThickness'].fillna(S_m)
X_test['Insulin'] = X_test['Insulin'].fillna(I_m)
X_test['BMI'] = X_test['BMI'].fillna(Bm_m )
In [37]:
X_test['Pregnancies'] = X_test['Pregnancies'].fillna(X_test['Pregnancies'].median())
In [38]:
X_test
Out[38]:
| Pregnancies | Glucose | BloodPressure | SkinThickness | Insulin | BMI | DiabetesPedigreeFunction | Age | |
|---|---|---|---|---|---|---|---|---|
| 44 | 7.0 | 159.0 | 64.0 | 23.0 | 30.5 | 27.4 | 0.294 | 40 |
| 672 | 10.0 | 68.0 | 106.0 | 23.0 | 49.0 | 35.5 | 0.285 | 47 |
| 700 | 2.0 | 122.0 | 76.0 | 27.0 | 200.0 | 35.9 | 0.483 | 26 |
| 630 | 7.0 | 114.0 | 64.0 | 23.0 | 30.5 | 27.4 | 0.732 | 34 |
| 81 | 2.0 | 74.0 | 72.0 | 23.0 | 30.5 | 32.0 | 0.102 | 22 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 32 | 3.0 | 88.0 | 58.0 | 11.0 | 54.0 | 24.8 | 0.267 | 22 |
| 637 | 2.0 | 94.0 | 76.0 | 18.0 | 66.0 | 31.6 | 0.649 | 23 |
| 593 | 2.0 | 82.0 | 52.0 | 22.0 | 115.0 | 28.5 | 1.699 | 25 |
| 425 | 4.0 | 184.0 | 78.0 | 39.0 | 277.0 | 37.0 | 0.264 | 31 |
| 273 | 1.0 | 71.0 | 78.0 | 50.0 | 45.0 | 33.2 | 0.422 | 21 |
154 rows × 8 columns
In [39]:
X_test.isna().sum()
Out[39]:
Pregnancies 0
Glucose 0
BloodPressure 0
SkinThickness 0
Insulin 0
BMI 0
DiabetesPedigreeFunction 0
Age 0
dtype: int64In [40]:
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_test_s = scaler.fit_transform(X_test)
X_test_s
Out[40]:
array([[ 0.76197764, 1.16484536, -0.8288433 , ..., -0.71876183,
-0.46562514, 0.63400979],
[ 1.72381827, -1.66920722, 2.88630463, ..., 0.4261539 ,
-0.49253293, 1.24533587],
[-0.84109008, 0.01253827, 0.23262754, ..., 0.48269295,
0.09943846, -0.58864236],
...,
[-0.84109008, -1.23319913, -1.89031414, ..., -0.56327945,
3.73497988, -0.67597466],
[-0.19986299, 1.94343123, 0.40953934, ..., 0.63817533,
-0.55531777, -0.15198088],
[-1.16170362, -1.57577692, 0.40953934, ..., 0.10105437,
-0.08293657, -1.02530385]])In [41]:
y_pred = clf.predict(X_test_s)
In [42]:
from sklearn.metrics import accuracy_score, recall_score, precision_score,f1_score
acc = accuracy_score(y_test,y_pred) # 정답값, 예측
print(f'optimal_accuracy: {acc}')
optimal_accuracy: 0.7402597402597403
모델 튜닝
C, gamma,kernel,degrees 하이퍼 파라미터 튜닝
In [43]:
from sklearn.model_selection import GridSearchCV
params = {
"C" : [0.1 ,1 ],
'gamma' : [0.01,0.1],
'degree' : [2,3],
'kernel' : ['linear','poly']
}
grid_cv = GridSearchCV(SVC(),params,cv=5,refit= True, verbose=3)
grid_cv.fit(X_train_s,y_train)
Fitting 5 folds for each of 16 candidates, totalling 80 fits
[CV 1/5] END C=0.1, degree=2, gamma=0.01, kernel=linear;, score=0.764 total time= 0.0s
[CV 2/5] END C=0.1, degree=2, gamma=0.01, kernel=linear;, score=0.756 total time= 0.0s
[CV 3/5] END C=0.1, degree=2, gamma=0.01, kernel=linear;, score=0.756 total time= 0.0s
[CV 4/5] END C=0.1, degree=2, gamma=0.01, kernel=linear;, score=0.780 total time= 0.0s
[CV 5/5] END C=0.1, degree=2, gamma=0.01, kernel=linear;, score=0.811 total time= 0.0s
[CV 1/5] END C=0.1, degree=2, gamma=0.01, kernel=poly;, score=0.650 total time= 0.0s
[CV 2/5] END C=0.1, degree=2, gamma=0.01, kernel=poly;, score=0.650 total time= 0.0s
[CV 3/5] END C=0.1, degree=2, gamma=0.01, kernel=poly;, score=0.650 total time= 0.0s
[CV 4/5] END C=0.1, degree=2, gamma=0.01, kernel=poly;, score=0.650 total time= 0.0s
[CV 5/5] END C=0.1, degree=2, gamma=0.01, kernel=poly;, score=0.656 total time= 0.0s
[CV 1/5] END C=0.1, degree=2, gamma=0.1, kernel=linear;, score=0.764 total time= 0.0s
[CV 2/5] END C=0.1, degree=2, gamma=0.1, kernel=linear;, score=0.756 total time= 0.0s
[CV 3/5] END C=0.1, degree=2, gamma=0.1, kernel=linear;, score=0.756 total time= 0.0s
[CV 4/5] END C=0.1, degree=2, gamma=0.1, kernel=linear;, score=0.780 total time= 0.0s
[CV 5/5] END C=0.1, degree=2, gamma=0.1, kernel=linear;, score=0.811 total time= 0.0s
[CV 1/5] END C=0.1, degree=2, gamma=0.1, kernel=poly;, score=0.634 total time= 0.0s
[CV 2/5] END C=0.1, degree=2, gamma=0.1, kernel=poly;, score=0.659 total time= 0.0s
[CV 3/5] END C=0.1, degree=2, gamma=0.1, kernel=poly;, score=0.650 total time= 0.0s
[CV 4/5] END C=0.1, degree=2, gamma=0.1, kernel=poly;, score=0.650 total time= 0.0s
[CV 5/5] END C=0.1, degree=2, gamma=0.1, kernel=poly;, score=0.656 total time= 0.0s
[CV 1/5] END C=0.1, degree=3, gamma=0.01, kernel=linear;, score=0.764 total time= 0.0s
[CV 2/5] END C=0.1, degree=3, gamma=0.01, kernel=linear;, score=0.756 total time= 0.0s
[CV 3/5] END C=0.1, degree=3, gamma=0.01, kernel=linear;, score=0.756 total time= 0.0s
[CV 4/5] END C=0.1, degree=3, gamma=0.01, kernel=linear;, score=0.780 total time= 0.0s
[CV 5/5] END C=0.1, degree=3, gamma=0.01, kernel=linear;, score=0.811 total time= 0.0s
[CV 1/5] END C=0.1, degree=3, gamma=0.01, kernel=poly;, score=0.650 total time= 0.0s
[CV 2/5] END C=0.1, degree=3, gamma=0.01, kernel=poly;, score=0.650 total time= 0.0s
[CV 3/5] END C=0.1, degree=3, gamma=0.01, kernel=poly;, score=0.650 total time= 0.0s
[CV 4/5] END C=0.1, degree=3, gamma=0.01, kernel=poly;, score=0.650 total time= 0.0s
[CV 5/5] END C=0.1, degree=3, gamma=0.01, kernel=poly;, score=0.656 total time= 0.0s
[CV 1/5] END C=0.1, degree=3, gamma=0.1, kernel=linear;, score=0.764 total time= 0.0s
[CV 2/5] END C=0.1, degree=3, gamma=0.1, kernel=linear;, score=0.756 total time= 0.0s
[CV 3/5] END C=0.1, degree=3, gamma=0.1, kernel=linear;, score=0.756 total time= 0.0s
[CV 4/5] END C=0.1, degree=3, gamma=0.1, kernel=linear;, score=0.780 total time= 0.0s
[CV 5/5] END C=0.1, degree=3, gamma=0.1, kernel=linear;, score=0.811 total time= 0.0s
[CV 1/5] END C=0.1, degree=3, gamma=0.1, kernel=poly;, score=0.659 total time= 0.0s
[CV 2/5] END C=0.1, degree=3, gamma=0.1, kernel=poly;, score=0.659 total time= 0.0s
[CV 3/5] END C=0.1, degree=3, gamma=0.1, kernel=poly;, score=0.699 total time= 0.0s
[CV 4/5] END C=0.1, degree=3, gamma=0.1, kernel=poly;, score=0.691 total time= 0.0s
[CV 5/5] END C=0.1, degree=3, gamma=0.1, kernel=poly;, score=0.730 total time= 0.0s
[CV 1/5] END C=1, degree=2, gamma=0.01, kernel=linear;, score=0.772 total time= 0.0s
[CV 2/5] END C=1, degree=2, gamma=0.01, kernel=linear;, score=0.748 total time= 0.0s
[CV 3/5] END C=1, degree=2, gamma=0.01, kernel=linear;, score=0.756 total time= 0.0s
[CV 4/5] END C=1, degree=2, gamma=0.01, kernel=linear;, score=0.772 total time= 0.0s
[CV 5/5] END C=1, degree=2, gamma=0.01, kernel=linear;, score=0.803 total time= 0.0s
[CV 1/5] END C=1, degree=2, gamma=0.01, kernel=poly;, score=0.642 total time= 0.0s
[CV 2/5] END C=1, degree=2, gamma=0.01, kernel=poly;, score=0.650 total time= 0.1s
[CV 3/5] END C=1, degree=2, gamma=0.01, kernel=poly;, score=0.650 total time= 0.0s
[CV 4/5] END C=1, degree=2, gamma=0.01, kernel=poly;, score=0.650 total time= 0.1s
[CV 5/5] END C=1, degree=2, gamma=0.01, kernel=poly;, score=0.656 total time= 0.0s
[CV 1/5] END C=1, degree=2, gamma=0.1, kernel=linear;, score=0.772 total time= 0.0s
[CV 2/5] END C=1, degree=2, gamma=0.1, kernel=linear;, score=0.748 total time= 0.0s
[CV 3/5] END C=1, degree=2, gamma=0.1, kernel=linear;, score=0.756 total time= 0.0s
[CV 4/5] END C=1, degree=2, gamma=0.1, kernel=linear;, score=0.772 total time= 0.0s
[CV 5/5] END C=1, degree=2, gamma=0.1, kernel=linear;, score=0.803 total time= 0.0s
[CV 1/5] END C=1, degree=2, gamma=0.1, kernel=poly;, score=0.659 total time= 0.0s
[CV 2/5] END C=1, degree=2, gamma=0.1, kernel=poly;, score=0.715 total time= 0.0s
[CV 3/5] END C=1, degree=2, gamma=0.1, kernel=poly;, score=0.683 total time= 0.0s
[CV 4/5] END C=1, degree=2, gamma=0.1, kernel=poly;, score=0.715 total time= 0.0s
[CV 5/5] END C=1, degree=2, gamma=0.1, kernel=poly;, score=0.656 total time= 0.0s
[CV 1/5] END C=1, degree=3, gamma=0.01, kernel=linear;, score=0.772 total time= 0.1s
[CV 2/5] END C=1, degree=3, gamma=0.01, kernel=linear;, score=0.748 total time= 0.0s
[CV 3/5] END C=1, degree=3, gamma=0.01, kernel=linear;, score=0.756 total time= 0.0s
[CV 4/5] END C=1, degree=3, gamma=0.01, kernel=linear;, score=0.772 total time= 0.0s
[CV 5/5] END C=1, degree=3, gamma=0.01, kernel=linear;, score=0.803 total time= 0.0s
[CV 1/5] END C=1, degree=3, gamma=0.01, kernel=poly;, score=0.642 total time= 0.0s
[CV 2/5] END C=1, degree=3, gamma=0.01, kernel=poly;, score=0.650 total time= 0.1s
[CV 3/5] END C=1, degree=3, gamma=0.01, kernel=poly;, score=0.650 total time= 0.0s
[CV 4/5] END C=1, degree=3, gamma=0.01, kernel=poly;, score=0.650 total time= 0.1s
[CV 5/5] END C=1, degree=3, gamma=0.01, kernel=poly;, score=0.656 total time= 0.1s
[CV 1/5] END C=1, degree=3, gamma=0.1, kernel=linear;, score=0.772 total time= 0.0s
[CV 2/5] END C=1, degree=3, gamma=0.1, kernel=linear;, score=0.748 total time= 0.0s
[CV 3/5] END C=1, degree=3, gamma=0.1, kernel=linear;, score=0.756 total time= 0.0s
[CV 4/5] END C=1, degree=3, gamma=0.1, kernel=linear;, score=0.772 total time= 0.0s
[CV 5/5] END C=1, degree=3, gamma=0.1, kernel=linear;, score=0.803 total time= 0.0s
[CV 1/5] END C=1, degree=3, gamma=0.1, kernel=poly;, score=0.707 total time= 0.0s
[CV 2/5] END C=1, degree=3, gamma=0.1, kernel=poly;, score=0.707 total time= 0.0s
[CV 3/5] END C=1, degree=3, gamma=0.1, kernel=poly;, score=0.691 total time= 0.0s
[CV 4/5] END C=1, degree=3, gamma=0.1, kernel=poly;, score=0.724 total time= 0.0s
[CV 5/5] END C=1, degree=3, gamma=0.1, kernel=poly;, score=0.779 total time= 0.0s
Out[43]:
GridSearchCV(cv=5, estimator=SVC(),
param_grid={'C': [0.1, 1], 'degree': [2, 3], 'gamma': [0.01, 0.1],
'kernel': ['linear', 'poly']},
verbose=3)On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
GridSearchCV(cv=5, estimator=SVC(),
param_grid={'C': [0.1, 1], 'degree': [2, 3], 'gamma': [0.01, 0.1],
'kernel': ['linear', 'poly']},
verbose=3)SVC()SVC()In [45]:
grid_cv.best_estimator_
Out[45]:
SVC(C=0.1, degree=2, gamma=0.01, kernel='linear')On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
SVC(C=0.1, degree=2, gamma=0.01, kernel='linear')In [46]:
grid_cv.best_score_ # 최고의 모델 정확도
Out[46]:
0.7736771957883513In [47]:
grid_cv.best_params_
Out[47]:
{'C': 0.1, 'degree': 2, 'gamma': 0.01, 'kernel': 'linear'}베스트 모델 학습
In [50]:
clf = SVC(C= 0.1, degree=2, gamma = 0.01, kernel = 'linear')
clf = clf.fit(X_train_s,y_train)
모델 저장
In [52]:
import pickle
with open('svc_c_1_degree_2_gamma_001_rbf.pickle','wb') as f:
pickle.dump(clf,f)
In [54]:
# 스케일러
with open('stanard_scaler.pickle','wb') as f:
pickle.dump(scaler,f)
저장된 모델 사용하기
In [ ]:
with open('/content/svc_c_1_degree_2_gamma_001_rbf.pickle','rb') as f:
c = pickle.read(f)
'AI > AI Project' 카테고리의 다른 글
| KNN으로 citrus data set 분류하기 (1) | 2024.01.30 |
|---|---|
| 사용자 MBTI 유추하기 프로젝트 (4) | 2023.12.05 |
| covid 데이터 선형회귀 (0) | 2023.09.13 |
| Spark MLLib Titanic Data - MulticlassClassification (0) | 2023.09.12 |
| Yolov5모델로 쓰레기 탐지하기 (0) | 2023.09.12 |