문제
준규는 N×M 크기의 미로에 갇혀있다. 미로는 1×1크기의 방으로 나누어져 있고, 각 방에는 사탕이 놓여져 있다. 미로의 가장 왼쪽 윗 방은 (1, 1)이고, 가장 오른쪽 아랫 방은 (N, M)이다.
준규는 현재 (1, 1)에 있고, (N, M)으로 이동하려고 한다. 준규가 (r, c)에 있으면, (r+1, c), (r, c+1), (r+1, c+1)로 이동할 수 있고, 각 방을 방문할 때마다 방에 놓여져있는 사탕을 모두 가져갈 수 있다. 또, 미로 밖으로 나갈 수는 없다.
준규가 (N, M)으로 이동할 때, 가져올 수 있는 사탕 개수의 최댓값을 구하시오.
입력
첫째 줄에 미로의 크기 N, M이 주어진다. (1 ≤ N, M ≤ 1,000)
둘째 줄부터 N개 줄에는 총 M개의 숫자가 주어지며, r번째 줄의 c번째 수는 (r, c)에 놓여져 있는 사탕의 개수이다. 사탕의 개수는 0보다 크거나 같고, 100보다 작거나 같다.
출력
첫째 줄에 준규가 (N, M)으로 이동할 때, 가져올 수 있는 사탕 개수를 출력한다.
예제 입력 1
3 4
1 2 3 4
0 0 0 5
9 8 7 6
예제 출력 1
31
예제 입력 2
3 3
1 0 0
0 1 0
0 0 1
예제 출력 2
3
예제 입력 3
4 3
1 2 3
6 5 4
7 8 9
12 11 10
예제 출력 3
47
문제 풀이
N,M = map(int,input().split())
matrix = []
for i in range(N): # 초기값 세팅
list1 = list(map(int,input().split()))
matrix.append(list1)
dx = [1,0,1]
dy = [0,1,1]
dp = [[0 for _ in range(M+1)] for _ in range(N+1)] # dp 초기 배열 설정
for i in range(1, N+1):
for j in range(1, M+1):
dp[i][j] = matrix[i-1][j-1] + max(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) # 점화식
print(dp[N][M])문제 접근
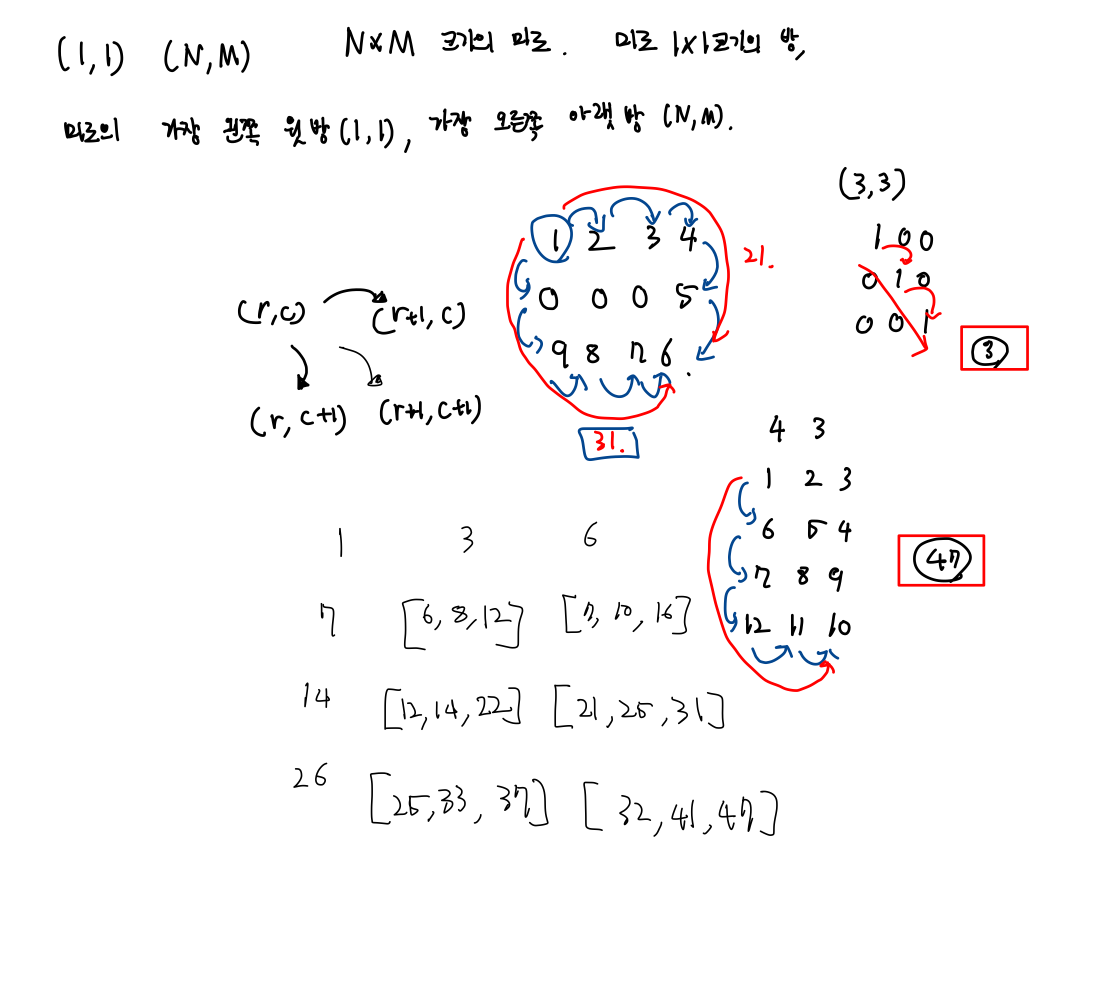
하나하나씩 우로 한칸, 밑으로 한칸, 오른쪽 대각선 한칸씩 값을 더하면 위 4*3 모양처럼 값들이 나오게 됩니다.
이때 값들 중 최대값을 구하기 때문에 리스트 안에 있는 값들 중 max함수를 사용하여 큰 값을 호출하여 이를 dp 리스트에 넣어 준후 N*M에 도달했을 때 값을 추출하면 됩니다.
추가적으로 dp를 그냥 +1을 안한상태에서 이중 리스트를 만들면 조건문을 통해 따로 예외처리를 해줘야 하기 때문에 편하게 계산하고자 +1을 더하였습니다.
'Algorithm > baekjoon' 카테고리의 다른 글
| Baekjoon [14569] 시간표짜기 - python (2) | 2023.01.26 |
|---|---|
| Baekjoon [3085] 사탕게임 - python (0) | 2023.01.25 |
| Baekjoon [1904] 01타일 - python (0) | 2023.01.17 |
| Baekjoon [14501] 퇴사 - python (0) | 2023.01.14 |
| Baekjoon [11057] 오르막 수 - python (0) | 2023.01.13 |
