반응형
해당 글은 (Day16 Linear Regression chap1)[https://sunho99.tistory.com/entry/4주차-Day16-딥러닝-기초-및-비전-chap1] 와 내용이 이어진다.
Linear Regression 바닥부터 구현(Bias 포함)
- Linear Regression을 Python만을 이용하여 구현합니다.
- 학습 목적의 데이터 준비
| 하루 노동 시간 | 하루 매출 |
|---|---|
| 1 | 25,000 |
| 2 | 55,000 |
| 3 | 75,000 |
| 4 | 110,000 |
| 5 | 128,000 |
| 6 | 155,000 |
| 7 | 180,000 |
- 목표: 하루 노동 시간이 8시간일 때 하루 매출은 얼마가 될까요?
import matplotlib.pyplot as plt
X = [1, 2, 3, 4, 5, 6, 7]
Y = [25000, 55000, 75000, 110000, 128000, 155000, 180000]
plt.plot(X, Y)
plt.scatter(X, Y)<matplotlib.collections.PathCollection at 0x7f50da7fab00>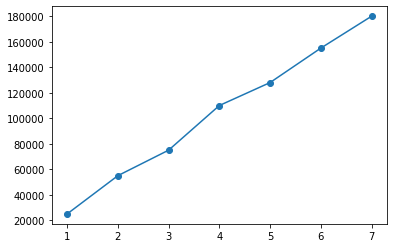
가설 클래스 정의
- Forward: 모델이 입력을 받아 정방향으로(왼쪽에서 오른쪽으로) 계산해 결과를 출력하는 과정
# 가설 모델(학습 시킬 대상)
class H():
def __init__(self, w, b):
self.w = w
self.b = b
# 결과를 반환하는 함수
def forward(self, x):
return self.w * x + self.b
# 가설의 비용을 구하는 함수(낮추어야 할 대상)
def get_cost(self, X, Y):
cost = 0
for i in range(len(X)):
cost += (self.forward(X[i]) - Y[i]) ** 2
cost = cost / len(X)
return cost
# 미분으로 기울기를 계산하는 함수
def get_gradient_using_derivative(self, X, Y):
w_gradient = 0
b_gradient = 0
for i in range(len(X)):
w_gradient += (self.forward(X[i]) - Y[i]) * X[i]
b_gradient += (self.forward(X[i]) - Y[i])
w_gradient = 2 * w_gradient / len(X)
b_gradient = 2 * b_gradient / len(X)
return w_gradient, b_gradient, self.get_cost(X, Y)
# w 값을 변경하는 함수
def set_w(self, w):
self.w = w
# w 값을 반환하는 함수
def get_w(self):
return self.w
# b 값을 변경하는 함수
def set_b(self, b):
self.b = b
# b 값을 반환하는 함수
def get_b(self):
return self.b학습 진행하기
- 기본적인 기울기 함수를 이용하여 학습을 진행합니다.
w = 4
b = 0
h = H(w, b)
learning_rate = 0.001
for i in range(10001):
w_gradient, b_gradient, cost = h.get_gradient_using_derivative(X, Y)
h.set_w(h.get_w() + learning_rate * -w_gradient)
h.set_b(h.get_b() + learning_rate * -b_gradient)
if i % 1000 == 0:
print("[ epoch: %d, cost: %.2f ]" % (i, cost))
print("w = %.2f, w_gradient = %.2f" % (h.get_w(), w_gradient))
print("b = %.2f, b_gradient = %.2f" % (h.get_b(), b_gradient))
print("f(x) = %.2fx + %.2f" %(h.get_w(), h.get_b()))
print("예측값: [%.2f]" %(h.forward(8)))[ epoch: 0, cost: 13450708891.43 ]
w = 1040.98, w_gradient = -1036982.86
b = 207.97, b_gradient = -207968.00
[ epoch: 1000, cost: 9835710.05 ]
w = 25147.86, w_gradient = -190.39
b = 3879.77, b_gradient = 942.78
[ epoch: 2000, cost: 9190190.40 ]
w = 25305.88, w_gradient = -129.61
b = 3097.25, b_gradient = 641.81
[ epoch: 3000, cost: 8891034.74 ]
w = 25413.46, w_gradient = -88.23
b = 2564.54, b_gradient = 436.92
[ epoch: 4000, cost: 8752395.88 ]
w = 25486.69, w_gradient = -60.06
b = 2201.89, b_gradient = 297.44
[ epoch: 5000, cost: 8688145.94 ]
w = 25536.55, w_gradient = -40.89
b = 1955.02, b_gradient = 202.48
[ epoch: 6000, cost: 8658370.34 ]
w = 25570.48, w_gradient = -27.84
b = 1786.96, b_gradient = 137.84
[ epoch: 7000, cost: 8644571.32 ]
w = 25593.59, w_gradient = -18.95
b = 1672.54, b_gradient = 93.84
[ epoch: 8000, cost: 8638176.39 ]
w = 25609.32, w_gradient = -12.90
b = 1594.66, b_gradient = 63.88
[ epoch: 9000, cost: 8635212.76 ]
w = 25620.02, w_gradient = -8.78
b = 1541.64, b_gradient = 43.49
[ epoch: 10000, cost: 8633839.31 ]
w = 25627.31, w_gradient = -5.98
b = 1505.54, b_gradient = 29.60
f(x) = 25627.31x + 1505.54
예측값: [206524.05]학습 결과
x_pred = [i for i in range(11)]
y_pred = [h.get_w() * i + h.get_b() for i in range(11)]
plt.plot(x_pred, y_pred)
plt.scatter(X, Y)<matplotlib.collections.PathCollection at 0x7f50da83fb00>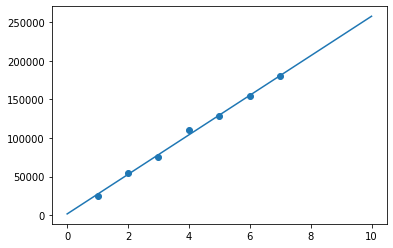
'AI_Bootcamp' 카테고리의 다른 글
| 4주차 Day17 Multivariable Linear Regression with PyTorch chap2 (0) | 2022.01.25 |
|---|---|
| 4주차 Day17 Linear Regression with PyTorch chap1 (0) | 2022.01.25 |
| 4주차 Day16 Linear Regression chap1 (0) | 2022.01.25 |
| 4주차 Day16 딥러닝 기초 및 비전 (0) | 2022.01.25 |
| 4주차 Day16 Numpy 심화 실습 2 (0) | 2022.01.24 |
