반응형
Linear Regression 바닥부터 구현
- Linear Regression을 Python만을 이용하여 구현합니다.
- 학습 목적의 데이터 준비
| 하루 노동 시간 | 하루 매출 |
|---|---|
| 1 | 25,000 |
| 2 | 55,000 |
| 3 | 75,000 |
| 4 | 110,000 |
| 5 | 128,000 |
| 6 | 155,000 |
| 7 | 180,000 |
- 목표: 하루 노동 시간이 8시간일 때 하루 매출은 얼마가 될까요?
import matplotlib.pyplot as plt
X = [1, 2, 3, 4, 5, 6, 7]
Y = [25000, 55000, 75000, 110000, 128000, 155000, 180000]
plt.plot(X, Y)
plt.scatter(X, Y)
가설 클래스 정의
- Forward: 모델이 입력을 받아 정방향으로(왼쪽에서 오른쪽으로) 계산해 결과를 출력하는 과정
# 가설 모델(학습 시킬 대상)
class H():
def __init__(self, w):
self.w = w
# 결과를 반환하는 함수
def forward(self, x):
return self.w * x
# 가설의 비용을 구하는 함수(낮추어야 할 대상)
def get_cost(self, X, Y):
cost = 0
for i in range(len(X)):
cost += (self.forward(X[i]) - Y[i]) ** 2
cost = cost / len(X)
return cost
# 기울기를 계산하는 함수
def get_gradient(self, X, Y):
cost = self.get_cost(X, Y)
dw = 0.001
self.w = self.w + dw
next_cost = self.get_cost(X, Y)
self.w = self.w - dw
dcost = next_cost - cost
gradient = dcost / dw
return gradient, next_cost
# 미분으로 기울기를 계산하는 함수
def get_gradient_using_derivative(self, X, Y):
gradient= 0
for i in range(len(X)):
gradient += (h.forward(X[i]) - Y[i]) * X[i]
gradient = 2 * gradient / len(X)
cost = self.get_cost(X, Y)
return gradient, cost
# w 값을 변경하는 함수
def set_w(self, w):
self.w = w
# w 값을 반환하는 함수
def get_w(self):
return self.w가중치(W)에 따른 비용 확인
- Forward: 모델이 입력을 받아 정방향으로(왼쪽에서 오른쪽으로) 계산해 결과를 출력하는 과정
cost_list = []
w_list = []
# w를 -300,000부터 300,000까지 바꾸어 보며 비용 확인
for i in range(-300, 300):
w = i * 1000
h = H(w)
cost = h.get_cost(X, Y)
w_list.append(w)
cost_list.append(cost)
# 결과적으로 약 25,000 정도일 때 최소 비용임을 확인
plt.figure(figsize=(8, 8))
plt.scatter(w_list, cost_list, s=10)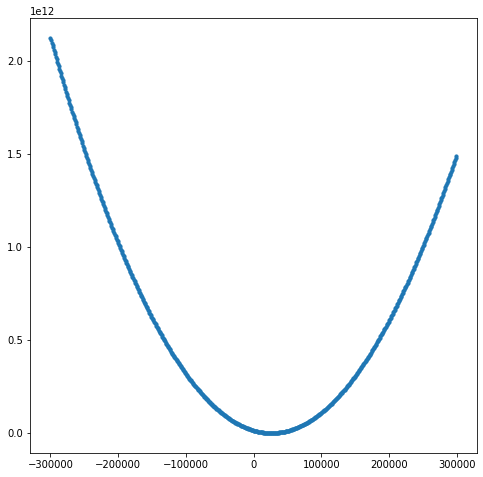
학습 진행하기
- 기본적인 기울기 함수를 이용하여 학습을 진행합니다.
w = 4
h = H(w)
learning_rate = 0.001
for i in range(1001):
gradient, cost = h.get_gradient(X, Y)
h.set_w(h.get_w() + learning_rate * -gradient)
if i % 100 == 0:
print("[ epoch: %d, cost: %.2f ]" % (i, cost))
print("w = %.2f, w_gradient = %.2f" % (h.get_w(), gradient))
print("f(x) = %.2fx" %(h.get_w()))
print("예측값: [%.2f]" %(h.forward(8)))[ epoch: 0, cost: 13450707854.45 ]
w = 1040.98, w_gradient = -1036982.84
[ epoch: 100, cost: 12866409.33 ]
w = 25508.71, w_gradient = -17494.23
[ epoch: 200, cost: 9041904.97 ]
w = 25921.49, w_gradient = -295.13
[ epoch: 300, cost: 9040816.63 ]
w = 25928.45, w_gradient = -4.98
[ epoch: 400, cost: 9040816.33 ]
w = 25928.57, w_gradient = -0.08
[ epoch: 500, cost: 9040816.33 ]
w = 25928.57, w_gradient = -0.00
[ epoch: 600, cost: 9040816.33 ]
w = 25928.57, w_gradient = -0.00
[ epoch: 700, cost: 9040816.33 ]
w = 25928.57, w_gradient = 0.00
[ epoch: 800, cost: 9040816.33 ]
w = 25928.57, w_gradient = 0.00
[ epoch: 900, cost: 9040816.33 ]
w = 25928.57, w_gradient = 0.00
[ epoch: 1000, cost: 9040816.33 ]
w = 25928.57, w_gradient = 0.00
f(x) = 25928.57x
예측값: [207428.57]- 편미분을 활용한 기울기 함수를 이용하여 학습해 봅시다.
w = 4
h = H(w)
learning_rate = 0.001
for i in range(1001):
gradient, cost = h.get_gradient_using_derivative(X, Y)
h.set_w(h.get_w() + learning_rate * -gradient)
if i % 100 == 0:
print("[ epoch: %d, cost: %.2f ]" % (i, cost))
print("w = %.2f, w_gradient = %.2f" % (h.get_w(), gradient))
print("f(x) = %.2fx" %(h.get_w()))
print("예측값: [%.2f]" %(h.forward(8)))[ epoch: 0, cost: 13450708891.43 ]
w = 1040.98, w_gradient = -1036982.86
[ epoch: 100, cost: 12866418.23 ]
w = 25508.71, w_gradient = -17494.23
[ epoch: 200, cost: 9041905.12 ]
w = 25921.49, w_gradient = -295.13
[ epoch: 300, cost: 9040816.64 ]
w = 25928.45, w_gradient = -4.98
[ epoch: 400, cost: 9040816.33 ]
w = 25928.57, w_gradient = -0.08
[ epoch: 500, cost: 9040816.33 ]
w = 25928.57, w_gradient = -0.00
[ epoch: 600, cost: 9040816.33 ]
w = 25928.57, w_gradient = -0.00
[ epoch: 700, cost: 9040816.33 ]
w = 25928.57, w_gradient = -0.00
[ epoch: 800, cost: 9040816.33 ]
w = 25928.57, w_gradient = -0.00
[ epoch: 900, cost: 9040816.33 ]
w = 25928.57, w_gradient = -0.00
[ epoch: 1000, cost: 9040816.33 ]
w = 25928.57, w_gradient = -0.00
f(x) = 25928.57x
예측값: [207428.57]학습 결과
x_pred = [i for i in range(11)]
y_pred = [h.get_w() * i for i in range(11)]
plt.plot(x_pred, y_pred)
plt.scatter(X, Y)
공부내용 정리
해당 코드는 선형회귀(Linear regression)에 대한 내용입니다.
선형회귀란 주어진 데이터를 학습시켜서 가장 합리적인 선형 함수를 찾아내는 접근 방법을 의미합니다.
이를 구현하기 위해선 가설함수 ex) H(x) = Wx + b등의로 예제 함수를 세우고 주어진 데이터를 이용하여 학습시켜 선형 함수를 수정해 나가는 것입니다.
이때 Cost를 줄이는 방향으로 학습을 진행하는데 Cost란 가설이 얼마나 정확한지 판단하는 기준입니다.
이 Cost를 구하기위해선 MSE(Mean Squared Error) 를 사용하여 계산합니다. 이때 Cost의 함수가 작성이 되는데 해당 점에서 Cost의 값이 최소가 되는 지점(값이 0)인 지점을 구하기 위해 경사 하강법(Gradient Descent) 를 사용하여 해당 Cost함수를 미분하게 됩니다.
그후 미분을 했을때의 기울기를 구한 후 그 기울기의 반대 방향으로 W를 업데이트 하며 값을 구하게 됩니다.
이때 너무 큰값을 이동하면 과하게 이동할 수 있으므로 학습률(Learning rate)를 곱하며 이동하게 됩니다.
개념 참고한 사이트
'AI_Bootcamp' 카테고리의 다른 글
| 4주차 Day17 Linear Regression with PyTorch chap1 (0) | 2022.01.25 |
|---|---|
| 4주차 Day16 Linear Regression with bias chap2 (0) | 2022.01.25 |
| 4주차 Day16 딥러닝 기초 및 비전 (0) | 2022.01.25 |
| 4주차 Day16 Numpy 심화 실습 2 (0) | 2022.01.24 |
| 4주차 Day16 Numpy 심화 실습 1 (0) | 2022.01.24 |
