반응형
Bubble Sort Algorithm
- 정렬 알고리즘 중 기본적인 알고리즘 중 하나로 인접한 두 숫자를 비교하여 두 수의 정렬 순서가 맞지 않은 경우에 swap을 하는 알고리즘입니다.
- 마치 깊은 물속의 큰 물방울이 표면으로 떠 오르는 것과 같이 큰 데이터들이 배열의 왼쪽에서 오른쪽으로 이동하기 대문에 bubble sort라고 부른다고 합니다.
- 해당 알고리즘은 stable한 Algorithm이면서, In-Place한 Algorithm입니다.
- Stable: 정렬 이후 입력된 순서 그래도 유지가 되는가?
- In-place: 데이터를 저장하는 메모리 이외는 상수 크기의 메모리만 필요하는가?
- 평균적인 시간 복잡도는 O(n^2)입니다.
- Pass
- 맨 왼쪽 인접한 두 숫자를 비교하기 시작합니다
- 맨 끝 인접한 두 숫자를 비교할 때까지 연속적으로 인접한 두숫자를 비교합니다
- 비교한 두 숫자의 정렬 순서가 맞지 않을 경우에는 교환합니다.
- Pass의 결과
- 제일 큰 숫자가 맨 오른족 끝으로 이동합니다
- 이 숫자는 더이상 다음 pass에 포함시기킬 필요가 없습니다
- 맨 왼쪽 인접한 두 숫자를 비교하기 시작합니다

Bubble Sort 연산과정
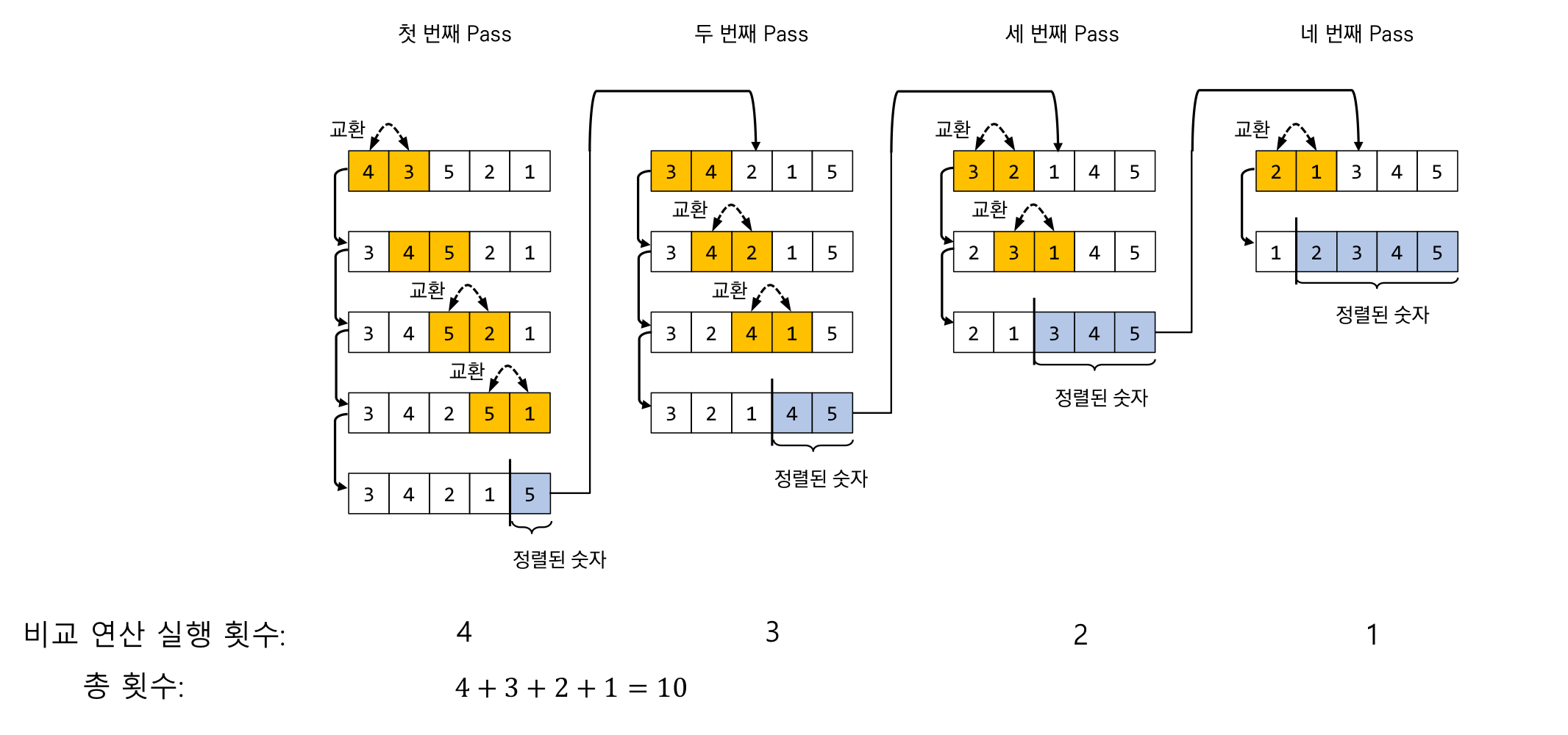
인접한 두 수의 크기를 비교합니다. 이때 비교 연산자의 실행 횟수는 입력 데이터가 n이라 가정하면 n(n-1)/2 의 연산회수가 나오게 됩니다.
이때 데이터의 위치 별로 부르는 별칭이 있습니다.
- 토끼 데이터 (rabbit data)
- 왼쪽에 있는 큰 데이터들은 빠르게 몇번의 pass를 통과하여 오른쪽 제위치로 이동하게 됩니다.
- 거북이 데이터 (turtle data)
- 오른쪽에 있는 작은 데이터 들은 매우 느리게 왼쪽 제 위치로 이동합니다.
Bubble Sort 코드
#include <stdio.h>
#include <iostream>
#define MAX_SIZE 1000
void bubbleSort(int a[], int n);
void bubbleSortImproved1(int a[], int n);
void bubbleSortImproved2(int a[], int n);
void copyArray(int a[], int b[], int n);
int main()
{
int numTestCases;
std::cin >> numTestCases;
for (int i = 0; i < numTestCases; ++i)
{
int num;
int a[MAX_SIZE], b[MAX_SIZE];
scanf("%d", &num);
for (int j = 0; j < num; j++)
scanf("%d", &b[j]);
copyArray(a, b, num);
bubbleSort(a, num);
copyArray(a, b, num);
bubbleSortImproved1(a, num);
copyArray(a, b, num);
bubbleSortImproved2(a, num);
printf("\n");
}
return 0;
}
void swap(int *a, int *b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
/* BubbleSort 함수 */
void bubbleSort(int a[], int n)
{
int countCmpOps = 0; // 비교 연산자 실행 횟수 int countSwaps = 0; // swap 함수 실행 횟수
int countSwaps = 0;
int len_a = sizeof(&a);
std::cout << len_a;
for(int pass = 1; pass < n; pass++){
for (int i = 1; i <= n - pass;i++){
countCmpOps ++;
if (a[i-1] > a[i]){
swap(&a[i-1],&a[i]);
countSwaps ++;
}
}
}
// bubble sort 알고리즘 구현
printf("%d %d ", countCmpOps, countSwaps);
return ;
}
/* BubbleSort 함수 - Improved Version 1 */ void bubbleSortImproved1(int a[], int n)
{
int countCmpOps = 0; // 비교 연산자 실행 횟수
int countSwaps = 0; // swap 함수 실행 횟수
// bubble sort의 개선된 알고리즘 (1) 구현
for (int pass = 1; pass < n; pass++)
{
bool swapped = false;
for (int i = 1; i <= n - pass; i++)
{
countCmpOps++;
if (a[i - 1] > a[i])
{
swap(&a[i - 1], &a[i]);
countSwaps++;
swapped = true;
}
}
if (swapped == false)
break;
}
printf("%d %d ", countCmpOps, countSwaps);
return ;
}
/* BubbleSort 함수 - Improved Version 2 */ void bubbleSortImproved2(int a[], int n)
{
int countCmpOps = 0; // 비교 연산자 실행 횟수
int countSwaps = 0; // swap 함수 실행 횟수
// bubble sort의 개선된 알고리즘 (2) 구현
int lastSwappedPos = n;
for (lastSwappedPos > 0;){
int swappedPos = 0;
for(int i=1;i<lastSwappedPos;i++){
if(a[i-1] > a[i]){
swap(&a[i-1],&a[i]);
swappedPos = i;
}
}
lastSwappedPos = swappedPos;
}
printf("%d %d ", countCmpOps, countSwaps);
return ;
}
void copyArray(int a[], int b[], int n)
{
for (int i = 0; i < n; i++)
a[i] = b[i];
}Cocktail Shaker Sort(Bidirectional bubble sort)
위 알고리즘은 Bubble Sort의 단점을 개선 시킨 알고리즘 입니다.
앞서 말했듯 거북이 데이터 즉, 오른쪽에 있는 작은 데이터들은 왼쪽으로 정렬하는데 오랜 시간이 걸리므로,
탐색을 진행할 때 왼쪽에서 오른쪽, 그다음엔 오른쪽에서 왼쪽 순으로 정렬탐색을 진행합니다..

'Algorithm > Concept' 카테고리의 다른 글
| [알고리즘 개념] Comb Sort (0) | 2022.10.22 |
|---|---|
| [알고리즘 개념] Selection Sort (1) | 2022.10.22 |
| [알고리즘 개념] 플로이드-워셜(Floyd-Warshall) 알고리즘이란? (0) | 2022.08.26 |
| [알고리즘 개념] Network Flow(네트워크 플로우) 최소 비용 최대 유량 (Minimum Cost Maximum Flow) Algorithm (0) | 2022.07.19 |
| [알고리즘 개념] Network Flow(네트워크 플로우) Edmonds-Karp Alogorithm (0) | 2022.07.18 |
