Network flow 개념
네트워크 플로우란 특정한 지점에서 다른 지점으로 데이터가 얼마나 많이 흐르고 있는가를 측정 할 수 있는 알고리즘입니다.
즉, 각 간선은 데이터가 흐를 수 잇는 정해진 용량으로 제한되어 있으며, 이를 최대한 양으로 얼마나 흐르게 할 수 있는 지 확인 할 수 있는 알고리즘입니다.
해당 vertex 사이의 간선에 최대용량 제한이 있다 생각하시면 되겠습니다.
예시를 들자면 물을 시작점에서 끝지점까지 흐를 때 얼마나 많은 물이 흐를 수 있는지, 또는 택배 물류 시스템 등으로도 사용 할 수 있습니다.
표현 방식은 주류 유량, 용량으로 표현합니다.
- flow network : 간선에 용량이라는 속성이 있는 그래프 입니다.
- source : 유량이 시작하는 정점입니다.
- sink : 유량이 도착해야하는 정점입니다.
- capacity : 각 간선에서 흐를 수 있는 flow의 최대 유량입니다. ex 1/4 or c(u,v) 등으로 표기합니다.
- flow : 각 간선에 대해서 다음 cnstraints를 만족하는 값 입니다. f(u,v)
- remaning amount : capacity에서 flow 값을 뺀 잔여량 입니다. (c(u,v) - f(u,v))
※ 3가지 특성
1. f(u,v) <= c(u,v) : 용량의 제한, 유량은 그 간선의 용량을 초과 할 수 없습니다.
2. f(u,v) = -f(v,u) : source 와 sink를 제외한 정점에는 들어오는 유량과 나가는 유량은 같습니다.
3. source에서 나오는 유량은 모두 sink로 흘러가므로 이는 소스에서 나오는 유량의 합과 같습니다.
표현 방식
주로 최대 유량을 구하기 위해선 모든 경우의수를 탐색하는 방법을 사용하며, 이때 주로 BFS 탐색 또는 DFS탐색을 하게 됩니다. 이 중 BFS로 탐색하는 방식을 Edmonds-Karp (에드몬드 카프) Algorithm이라고 합니다.
유량 상쇄
유량 상쇄는 모든 경로에, 기존에 존재하는 간선들과 반대되는 방향의 간선을 추가 한후, 기존 간선의 일정 유량이 흘러간다는 상황이 주어졌을 때, 음이 유량을 흘려보냄으로써, 간선사이의 유량을 상쇄 시키는 것을 의미합니다.
해당 내용이 이해가 잘 가지 않을 수 있지만, 이 부분을 이해해야 Network flow 알고리즘 중 하나인 Edmonds-Karp Algorithm을 이해 할 수 있습니다.
추가적으로 설명을 하자면 a -> b의 간선이 존재한다 가정 했을 때, 유량 f(a,b)가 1, 용량 c(a,b)가 1이라 가정했을 때, 역간선 b -> a의 유량 f(b,a)는 -1이 됩니다. 또한 용량 c(b,a)는 실제 존재하지 않은 간선이므로 0이 됩니다. 따라서 역간선 b -> a 의 잔여 용량은 0 - (-1) = 1 이 됩니다.
설명
네트워크 플로우의 개념을 그림으로 표현해봤습니다.

해당 그래프에 대해 설명을 하자면 a 가 시작점, f가 도착점입니다.
각 간선에 표시된 값은 [유량 / 용량] 입니다.
접근 방식
최대 유량을 구하기 위해선, 시작부터 종점까지 가능한 경로사이의 최소 유량 구하기, 현재상태를 업데이트 하는 과정
즉 이 2가지를 진행 해야 합니다.
먼저 node들 사이의 경로를 구하기 위해선 bfs로 탐색을 해야 합니다. 이때 다른 bfs관련된 graph문제들처럼 해당 node를 중복으로 접근하지 않기 위해 visited 등 변수 하나를 생성하여 관리를 해줍니다. 이때 다른 bfs와 다른점은 추후 간선들 사이의 유량을 구할 때 현재 상태를 업데이트 하며 경로를 따라가기 때문에 1 또는 0이 아닌, 해당 node를 오기 전 경로상의 직전 노드를 저장합니다.
이후 탐색을 하기 위해서 조건을 만족한다 가정하에 탐색하는데 , 보통 bfs를 탐색할 때는 node들이 방문했던 node들인지, 또는 벽이나 범위값을 벗어나지 않은지에 대해 조건문을 만들어 진행하지만, 이땐 현재의 flow가 해당 간선의 최대 flow인지와 한번도 방문하지 않았던 node인지가 조건이 됩니다.
에드몬드-카프 알고리즘 (Edmonds-Karp Algorithm)
해당 그래프가 있다 가정하겠습니다. 이때 모든 간선들의 유량을 0으로 초기화 합니다.
이후 만약 bfs를 바탕으로 탐색을 진행하며, 음의 간선을 모른다고 가정했을 때 결과값을 생각해 보겠습니다.
먼저 해당 용량을 가진 그래프를 바탕으로 진행하겠습니다.

- 경로 탐색은 해당 방식으로 진행됩니다.
- 1. 증가 경로를 찾습니다.
- 2. 찾아낸 경로에 보낼 수 있는 최대 flow를 찾습니다.
- 3. 찾아낸 경로에, 찾아낸 최대 flow를 사용합니다.
해당 이미지 처럼
a -> b -> e -> h 방식으로 3의 유량을 보내고,
a -> c -> e -> h 방식으로 2의 유량을 보내고,
a -> f -> g -> h 방식으로 4의 유량을 보내고,
이러면 총 9의 유량을 보낸다고 볼 수 있습니다. 하지만 실제로는 9의 유량이 아닌 10의 유량까지 보낼 수 있습니다.

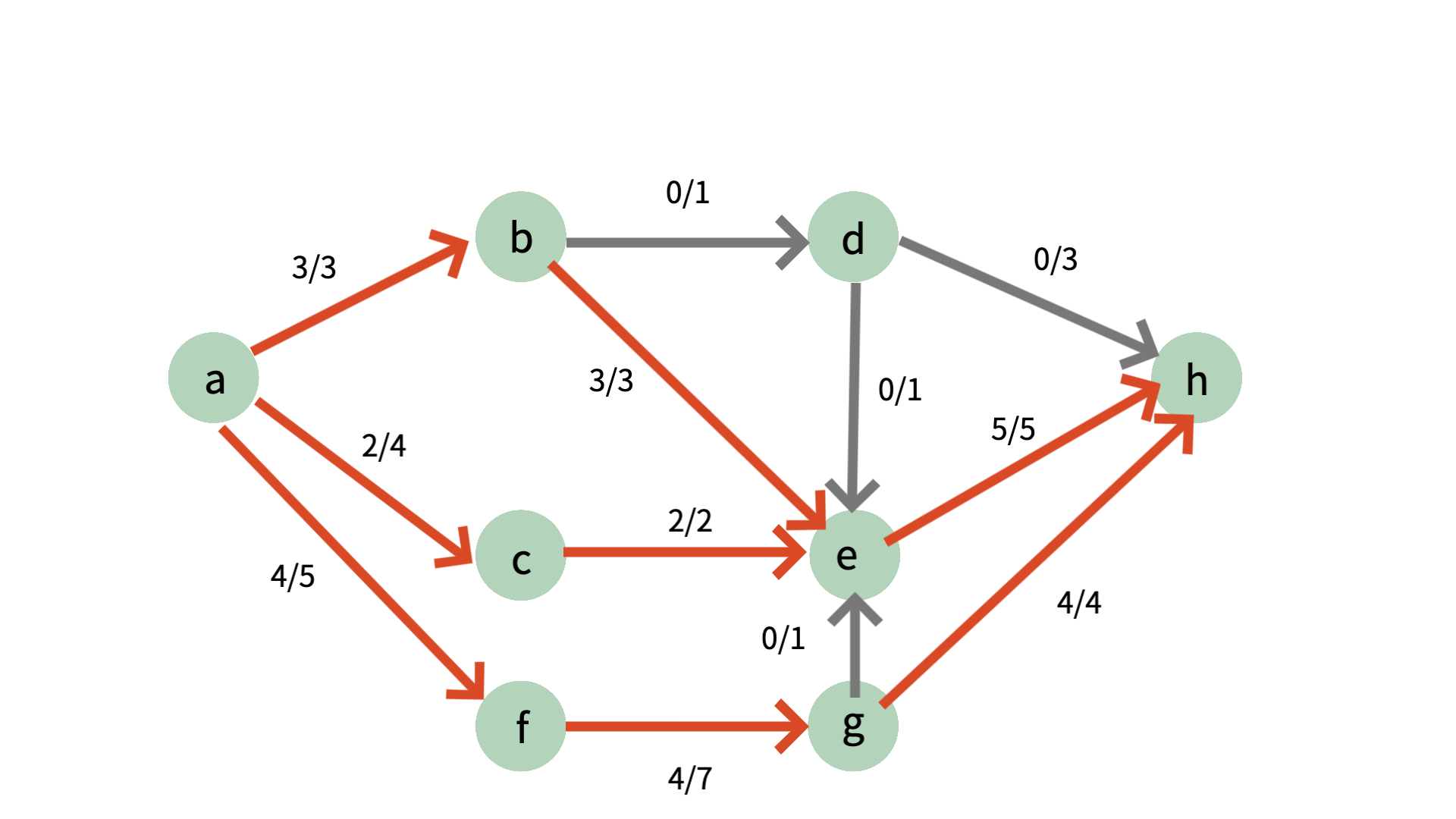
해당 이미지 처럼 총 10의 유량을 보낼 수 있게 됩니다.
a -> b -> e -> h 방식으로 2의 유량을 보내고,
a -> b -> d -> h 방식으로 1의 유량을 보내고
a -> c -> e -> h 방식으로 2의 유량을 보내고,
a -> f -> g -> h 방식으로 4의 유량을 보내게 됩니다.
이처럼 음의 간선을 이용하면 총 10의 유량을 보낼 수 있게 됩니다. 더 자세히 설명하자면

해당 f(b,e)에 음의 간선을 만듭니다. 이때 음의 간선은 용량 0, 유량 -3이라 가정합니다.
즉 c(b,e) 는 0, f(b,e)는 -3 입니다. 이때 f(a,f)에서 1의 유량이 더 흘러나오므로 정방향 flow 는 + 를 하고, 역방향 flow는 - 를 진행합니다.
이렇게 진행하면서 더 이상 잔여 용량이 남은 경로에 존재하지 않을 때까지 반복 진행합니다.
참고: https://binaryjourney.tistory.com/m/161 , https://www.zerocho.com/category/Algorithm/post/5893405b588acb00186d39e0, https://iknoom.tistory.com/13
'Algorithm > Concept' 카테고리의 다른 글
| [알고리즘 개념] Comb Sort (0) | 2022.10.22 |
|---|---|
| [알고리즘 개념] Selection Sort (1) | 2022.10.22 |
| [알고리즘 개념] Bubble Sort (0) | 2022.10.22 |
| [알고리즘 개념] 플로이드-워셜(Floyd-Warshall) 알고리즘이란? (0) | 2022.08.26 |
| [알고리즘 개념] Network Flow(네트워크 플로우) 최소 비용 최대 유량 (Minimum Cost Maximum Flow) Algorithm (0) | 2022.07.19 |
